Click here👆to get an answer to your question ️ If y^x = x^y , then find dy/dx Join / Login > 12th > Maths > Continuity and Differentiability > Logarithmic Differentiation > If y^x = x^y , then find d maths If y x = x y, then find d x d y ⇒ x y 1 d x d y lo g y × 1 = x y If y = log √(tan x), then the value of dy/dx at x = π/4 is given by A ∞ B 1 C 0 D 1/2 asked Apr in Differentiation by Kaina ( 304k points) differentiationTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `x^y=y^x`,then find` dy/dx`

If Y X 1 X 1 X 1 X Dot Prove That Dy Dx Y 2y X
Y=cos(1-x) find dy/dx
Y=cos(1-x) find dy/dx-(Your answers should be numbers or plus or minus infinity For plus infinity enter "PINF";//wwwquoracom/HowdoIsolvethisequationfracdydxleftfracxy1x2right2 Let u = (y x 1)^ (1) so u'= (yx1)^ (2) (y'1) = u^2 (x2)^ (2) This is a Riccati Eqn It can be converted to a linear 2nd order ode with the definition u= w'/w From that we have u'= w''/w




Find Dy Dx When Y X Raise To Power 1 X Brainly In
Let's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 logFind the particular solution of the differential equation dy/dx=1 x y xy, given that y = 0 when x = 1 I'll start with the second one for you Take the natural logarithm of both sides ln(x^y * y^x) = ln(1) ln(x^y) ln(y^x) = 0 yln(x) xln(y) = 0 dy/dxln(x) y/x ln y x/y(dy/dx) = 0 dy/dx(lnx x/y) = lny y/x dy/dx= (lny y/x)/(lnx x/y) dy/dx= (ln y y/x)/(lnx x/y) Now for the second I would differentiate term by term Let t = x^y and u = y^x Then lnt = ln(x^y) and lnu
So, by the chain rule dy/dx = (dy/du) * (du/dx) = y * ln (x)1) So dy/dx = ln (x)1 * x^x Next, let y# = x^x^x, which by convention is equal to x^ (x^x) not (x^x)^x) That is, exponentiation is carried out from right to left, not left to right, the opposite for the convention for subtraction and divisionFind dy/dx y=1/x y = 1 x y = 1 x Differentiate both sides of the equation d dx (y) = d dx ( 1 x) d d x ( y) = d d x ( 1 x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Rewrite 1 x 1 x as x − 1 x 1F' (x) = a n xn1 y = ex dy/dx = ex y = ea x dy/dx = a ea x y = ax dy/dx = ax ln (a) y = ln (x) dy/dx = 1 / x
If Y 3x 1 3x 1 Sin X Loge 1 X X 1 Then At X 0 Dy Dx Is Equal To If Y Cos 2 X Sec 2 X Then If Y Eq X X2 Plus X3 X4 Then The Value Of X Will Be If y is a function of x and log(x y) = 2xy, then the value of y'(0) is If y sec x tan x x 2 y = 0, then dy/dx = If Y Sinn X Cos Nx Then Dy Dx Is Equal To If Y X 3 5 And X Changes From 3 To 2 99Y x Differentials Given the function y = f(x) the derivative is dy dx = f0(x) However, we can treat dy/dx as a fraction and factor out the dx dy = f0(x)dx where dy and dx are called differentialsIfdy/dx can be interpreted as "the slope of a function", then dy is the "rise" and dx is the "run" Another way of looking at it is as$$\frac{d}{dx}(x^y)=yx^{y1}x^y\ln(x)\cdot\frac{dy}{dx},\qquad \frac{d}{dx}(y^x)=y^x\ln(y)xy^{x1}\cdot\frac{dy}{dx}$$ This may be hard to see but let's look at it another "way" (more of a physicist point of view)




Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com




Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com
This Video Learns About The Finding dy/dx If Function Is Given Asx ^y y ^x = 1This Problem Is Taken From The Book NCERTIt Is Board Model Problem Find dy/dx if y = x cot^(1) (x/y) Updated On To keep watching this video solution for FREE, Download our App Join the 2 Crores Student community now!Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is a




How Do You Find Dy Dx Of Tan X Y 1 Y Sqrt X 1 By Implicit Differentiation Homeworklib




If Y Xcot X 2x2 3 X2 X 2 Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Palrsebb
4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub in for y and then we have an answer for dy/dx Recall y=2^x (from our original question) So we get dy/dx = (2^x)(log(2)) => our final solutionIn Introduction to Derivatives (please read it first!) we looked at how to do a derivative using differences and limits Here we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by Δy dy/dx = (x 1)(x4)/(x1)(x4)1/(x1) 1/(x4) 1/(x1) 1/(x4) Stepbystep explanation Here, we want to find the derivative using logarithmic differentiation What we will do here is to first take the natural logarithm of both sides, then we proceed to differentiate afterwards



Q Tbn And9gcq69xqaiwgxy95 44f5sqsm2pnlgxvor Roue6xadfczqpkv4qx Usqp Cau



What Is The Derivative Of X Xy Y 1 Quora
Ex 53, 11 Find 𝑑𝑦/𝑑𝑥 in, 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) , 0 < x < 1 𝑦 = cos–1 ((1− 𝑥^2)/( 1 𝑥2 )) Putting x = tan θ yRecognize this is of the form u/v where u = ln x^2 and v = 3x1 Looking at the form we see it is a quotient and so we should apply the quotient rule Ex 94, 3 For each of the differential equations in Exercises 1 to 10, find the general solution 𝑑𝑦/𝑑𝑥𝑦=1 (𝑦≠1) 𝑑𝑦/𝑑𝑥𝑦=1 𝑑𝑦/𝑑𝑥=1−𝑦 𝑑𝑦 = (1 − y) dx 𝑑𝑦/ (1 − 𝑦) = dx 𝑑𝑦/ (𝑦 − 1) = −dx Integrating both sides ∫1 〖𝑑𝑦/ (𝑦 − 1)=〗 ∫1 〖−𝑑𝑥〗 log (y − 1) = −x C y − 1 = e (−x C) y − 1 = e−x × eC y = e−x × eC 1 Putting eC = A y = Ae−x 1 is the general solution




Find Dy Dx For The Given Function Y X 1 X 2 X Brainly In




If Y 1 Sqrt A 2 X 2 Find Dy Dx
Implicit\derivative\\frac{dx}{dy},\e^{xy}=e^{4x}e^{5y} implicitderivativecalculator en Related Symbolab blog posts High School Math Solutions – Derivative Calculator, Trigonometric Functions In the previous posts we covered the basic algebraic derivative rules (click here to see previous post) But howFind dy/dx by implicit differentiation tan (xy) = y/ (2x^2) 1 Educator answer Math Latest answer posted at 924 AM y (x) = (6/7)*e^ (7*x) (6/7) Stepbystep explanation I will use the notation dy/dx = y' We have y' 7*y = 6 Because in the right side we do not have any term that depends on x, we can assume that y is an exponential function y = a*e^ (b*x) c where a, b and c are constants



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora



If Y X Is A Solution Of 2 Sinx 1 Y Dy Dx Cosx And Y 0 1 Then Find The Value Of Y P 2 Studyrankersonline
If y= ln x^2/(3x1), how do I find dy/dx?5) d dx x x x () 10 10 1 g32 g16 6) If y = log x then dy dx = 1 x 7) If y = e 2 then dy dx = 2e 8) The derivative of a x is a xloga 9) The derivative of x m y n = (xy) (mn) is x y QIV Solve the following 1) If y = (6 x 3 − 3 x 2 −9 x) 10, find dy dx 2) If y = 3 8 5 2 4 5 x x g14 g14 g11 g12, find dy dx 3) If y = log(log(logx)) 2If Y = Sin1 X Cos1x Find (Dy)/(Dx) CBSE CBSE (Commerce) Class 12 Question Papers 1786 Textbook Solutions Important Solutions 3417 Question Bank Solutions Concept Notes & Videos 532 Time Tables 18 Syllabus Advertisement Remove all ads
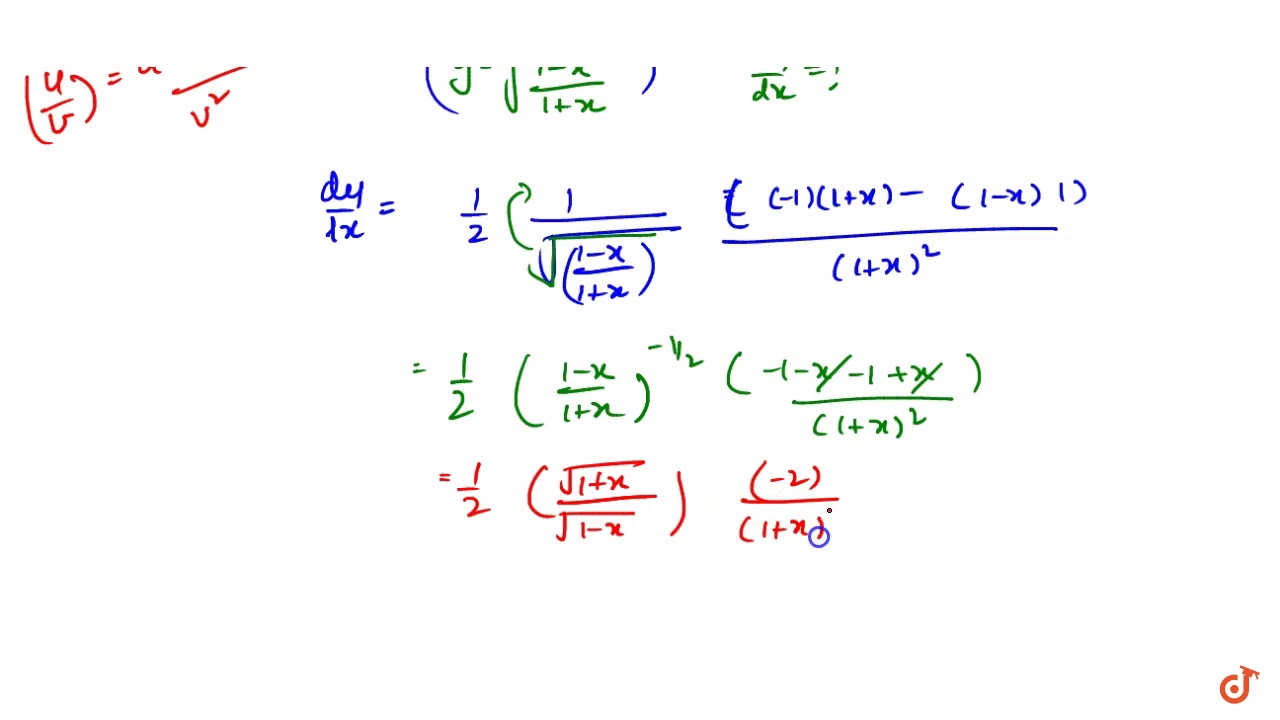



If Y Sqrt 1 X 1 X Then Dy Dx Equals Youtube




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12
Answer to Find dy/dx by implicit differentiation and evaluate the derivative at the given point (x_0, y_0) 2 x^3 y x y^2 = x, (x_0, y_0) = (1,Equalling the red y curve and the blue x curve happens also only in (1,1) and shows that dy/dx = dx/dy = 1 Now for z=z(x,y) Equalling the blue and greenFind dy/dx by implicit differentiation xe^y = x y Boost your resume with certification as an expert in up to 15 unique STEM subjects this summer




Find Dy Dx For Y X 3 Squareroot X 1 3x 2 2 Chegg Com




Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com
Transcribed image text Use logarithmic differentiation to find dy/dx y = (x 1)(x 8)/(x 1)(x 8), x > 8 dy/dx =In index notation, we have (sin x) y = x Taking natural logarithm on both sides yields y ln(sin x) = ln x Differentiating with respect to x yields y cos x sin x ln(sin x) dy dx = 1 x ⇒ y cot x ln(sin x) dy dx = 1 x Therefore, dy dx = (1 x − y cot x) 1 ln(sin x) iii) Given y = log x (cos 3 x) In index notation, we have x y = cos 3 xFind dy/dx of y = a^x To differentiate a function of the form y=a^x you need to use a neat little trick to rewrite a^x in the form of something you already know how to differentiate Using the fact that e^ln(x) is equal to x, y = a^x can be written as e^(ln(a)^x) Using log rules ln(a)^x can be written as xlna so now y can now be expressed as y



How Can We Solve The Differential Equation Dy Dx Y X 1 Quora




Y Log 1 X 1 X Find Dy Dx Brainly In
Answer to Find dy/dx y = x x1 By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask yourWatch Video in App This browser does not support the video element 100 000 Answer Find dy/dx for the given functiony=(x1)(x2)/√x 2 See answers brunoconti brunoconti Answer Stepbystep explanation BRAINLIEST BRAINLIEST BRAINLIEST Sanjuda Sanjuda 2 from the following figure find ML ABC A 60 B find the value of A in addition 41A 1 = 591 Solve 5p1=9 by Trans posing method Previous




Lesson 40 Derivatives Of Secondary Trig Functions Inverse




2 X2 4 1 X2 2x 4 X X2 2x Novocom Top
Active Oldest Votes 2 Assuming a is a constant then y ′ ( x) = d d x ( a 2 x − a x 2) = d d x ( a 2 x) − d d x ( a x 2) = a 2 d d x ( x) − a d d x ( x 2) = a 2 − 2 a x Then evaluate at x = 1 y ′ ( 1) = a 2 − 2 a Share answered Jan 29 '17 at 2348 kmeis if y = log tan (∏/4 x/2) show that dy/dx = sec x donot go shortcut if y = log (x (1 x 2) 1/2 ) prove that dy/dx = 1/log (x (1 x 2) 1/2) 1/ (1 x 2) 1/2 Find dy/dx y = x x e (2x 5) mention each and every step Find dy/dx (x) 1/2 (y) 1/2 = (a) 1/2 Mention each and every step If y = tan 1 a/x log (xa/xa) 1/2, proveFind dy/dx y=x \sin x^{2} 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨




If Y 3 U 2 U And U 4x 1 X 2 Find Dy Dx Brainly In
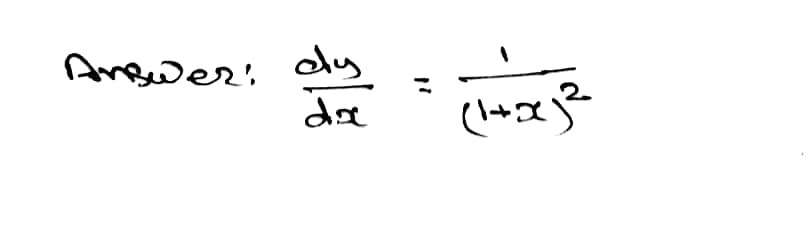



9 Y X 1 X Find Dy Dx Gauthmath
Best answer Given, xy = yx Taking logarithm on both sides, we get y log x = x log y Differentiating both sides, wrt x y (1/x) log x (dy/dx) = x (1/y) (dy/dx) log y 1 (y/x) (log x) (dy/dx) = (x/y) (dy/dx) log y (dy/dx) log x (x/y) = log y (y/x) (dy/dx) (y log x x)/y = (x log y y)/x राजेश की दुकान में दर्जन कमीजें , 15 दर्जन पैंट और 25 दर्जन जोड़ी मोजे हैं । यदि एक कमीज , एक पैंट और एक जोड़ी मोजे का मूल्य क्रमशः RsCalculus Find dy/dx y= (x1)/ (x2) y = x 1 x 2 y = x 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( x 1 x 2) d d x ( y) = d d x ( x 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps
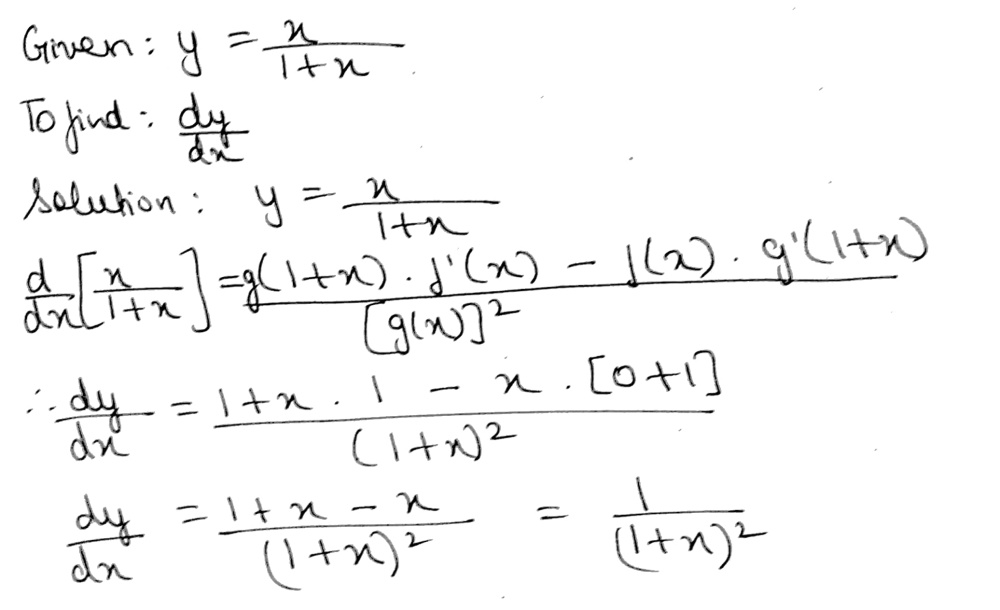



Ample 9 If Y X 1 X Find Dy Dx Ution Gauthmath




Umm Al Qura University Ppt Download
`dy/dx=1/(xy log10)cdot(yx cdot dy/dx)` In the line above we have applied the chain rule because `log(xy)` is a composite function On top of that we have applied product rule for `xy` to getIf y = x x and x > 0 then ln y = ln (x x) Use properties of logarithmic functions to expand the right side of the above equation as follows ln y = x ln x We now differentiate both sides with respect to x, using chain rule on the left side and the product rule on the right y '(1 / y) = ln x x(1 / x) = ln x 1 , where y ' = dy/dx MultiplyFor minus infinity enter "MINF") The solution is defined on the interval > x >




Find Dy Dx If Y Cos X X Sin X 1 X Brainly In




If Y Tan 1 1 X 1 X Find Dy Dx
The differential equation of the form is given as d y d x = y x Separating the variables, the given differential equation can be written as 1 y d y = 1 x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of theA Find y in terms of x if dy and y(0) = 7 dx y(x) = B For what xinterval is the solution defined? BTW, your original thread title was "Determine dy/dx of y=(x^5)^lnx" I changed "of" to "if" because you don't take "dy/dx" of something This symbol already represents the derivative of y with respect to x



How To Solve Dy Dx 1 Xy Y X Quora




If Y Sqrt 1 X 1 X Find Dy Dx And Prove That 1 X 2
619 unscientific said That makes absolute sense If a function is zero for all x,y then the infinitesimal change df would be 0 for all x,y In this problem you shouldn't think of f as identically 0 Here's an example to think about Suppose y=x (defining a curve) Take f (x,y)=x^2y^2 Then f (x,y)=0 along the line y=x, but f (x,y) is not This is the function y = x 3 2x 1 Its derivative is 3x 2 2 And it passes through the point (1,4) And now for the graph of the function, We can see that it passes through (1,4) We were given the `dy/dx` expression and we have found the "y = " expression and we can graph it And it's a cubic Music



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau




Ex 5 3 14 Find Dy Dx In Y Sin 1 2x Root 1 X2 Cbse




Ex 5 3 10 Find Dy Dx In Y Tan 1 3x X3 1 3x2 Ex 5 3



4 2 Implicit Differentiation




Find Dy Dx If Y Tan Inverse Square Root Of 1 X 2 Square Root Of 1 X 2 Square Root Of Maths Continuity And Differentiability Meritnation Com
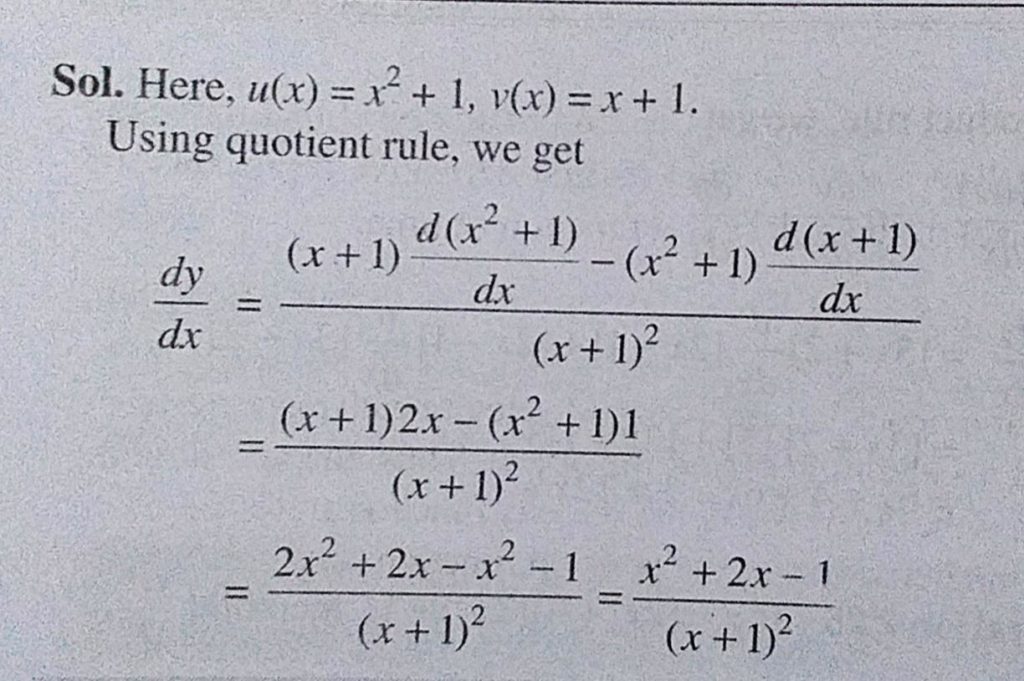



If Y X 2 1 X 1 Then Find Dy Dx Sahay Lms




If Y X 1 X 1 Then What Is Dy Dx Equal To
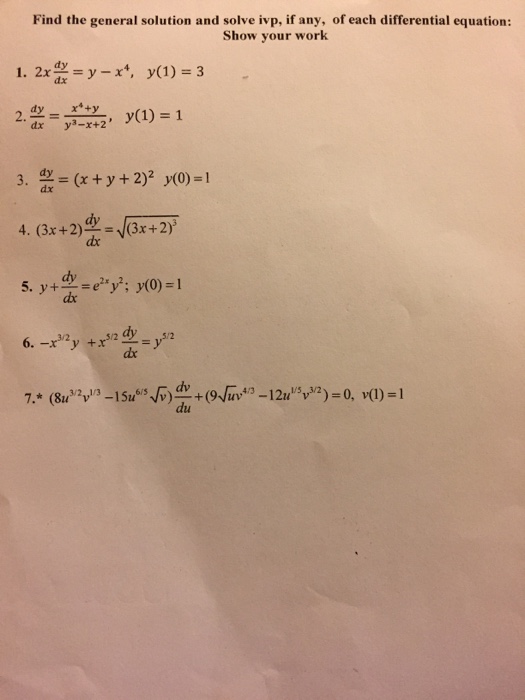



Find The General Solution And Solve Ivp If Any Of Chegg Com




Answered Use Logarithmic Differentiation To Find Bartleby




Assignment 1 If Y Xsinx Find Dx Dy 2 If Y Chegg Com



Www Math Colostate Edu Clayton Teaching M113f10 Homework Hw7solutions Pdf




If Y X 1 X Show That 2x Dydx Y 2 X




Implicit Differentiation How To Find Dy Dx 1 X 1 Y 3 Youtube



Http Www Thphys Physics Ox Ac Uk People Jamesbinney Mt Pdf




Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert




If Y X 1 X 1 X 1 X Dot Prove That Dy Dx Y 2y X




Find Dy Dx Y X X 1 X Brainly In




Find Dy Dx For Y X 3 Squareroot X 1 A 3x 2 2 Chegg Com



Given Y X 1 X Find Dy Dx From First Principl Gauthmath




Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com




If Y X A A X How Can You Prove That 2xy Dy De X A A X Quora




Solve X X 1 Dy Dx Y X2 X 1 2 Maths Differential Equations Meritnation Com




Misc 13 Find Dy Dx If Y Sin 1 X Sin 1 Root 1 X2 Miscellaneous




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Find Dy Dxof Y X Logx Log X X Socratic



If Tan 1 X Y Y Cot X 1 Then Find Dy Dx Sarthaks Econnect Largest Online Education Community



Initial Value Problem Dy Dx Y 1 X 3 With Y 1 0 Separable Differential Equation Youtube
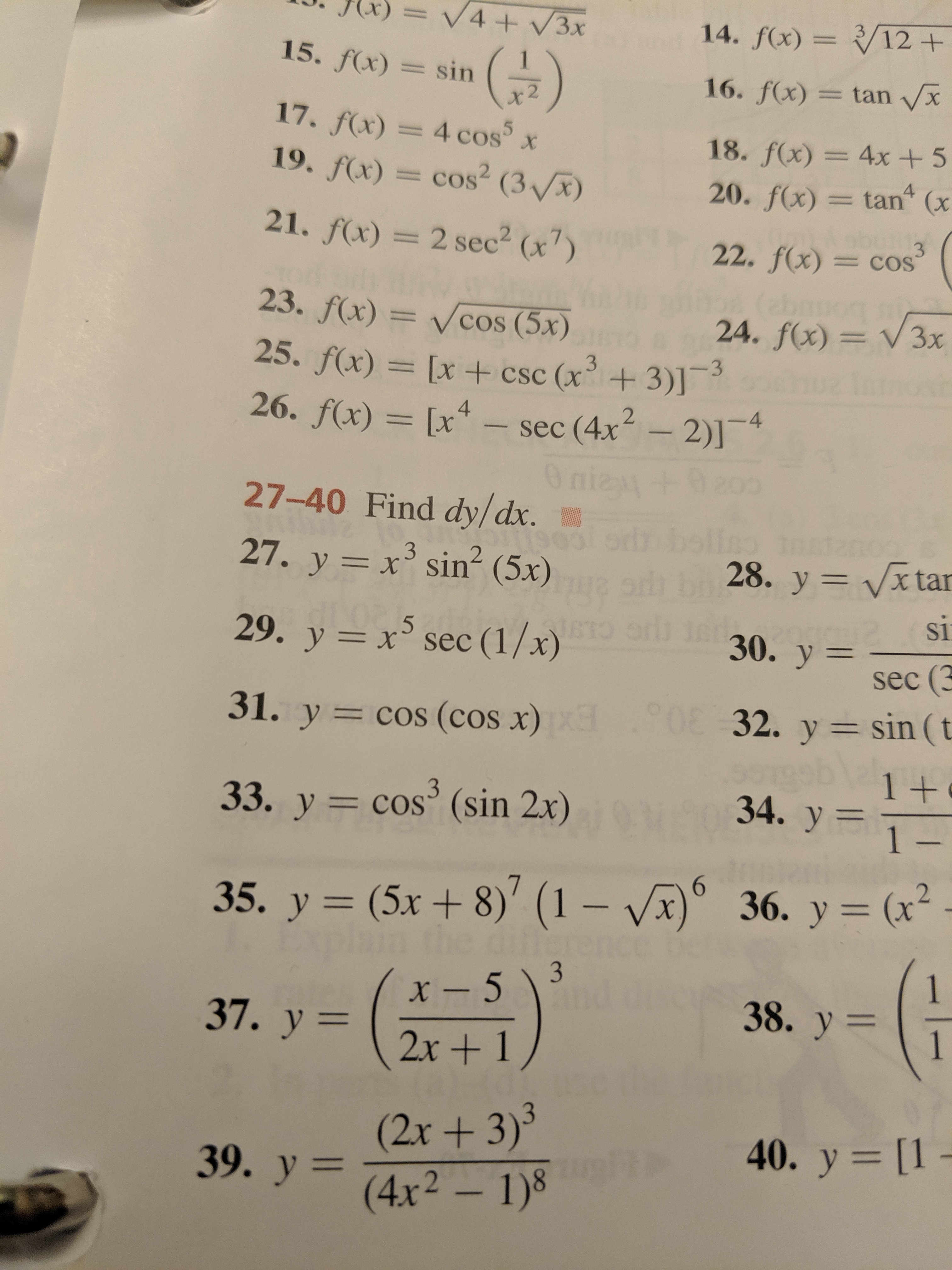



Answered V4 3x 14 F X 12 15 F X Sin 16 Bartleby




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange



What Is The Derivative Of X Y Y X 11 Quora




Solve X Dy Dx Y X 1 Ex Brainly In




Find Dy Dx When Y X Raise To Power 1 X Brainly In




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection



How To Solve The Equation Dy Dx 1 X Y X Y Quora




Find Dy Dx Y X 2 1 3 2x 1 Sqrt X 3 4x 1




If Y X 2 2x 3x 4 Then Find Dy Dx




If Y Cosx X Sin Inverse Root 3x Find Dy Dx Maths Continuity And Differentiability Meritnation Com




Find Dy Dx Of X Cos Y Sin X Y Socratic




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic



Find Dy Dx If Y Xtanx X2 1 2 Studyrankersonline




Differentiate The Function With Respect To X X Xcosx X 2 1 X 2 1 Mathematics Shaalaa Com




Find Dy Dx If Y Tan 1 A X 1 Ax Wyzant Ask An Expert
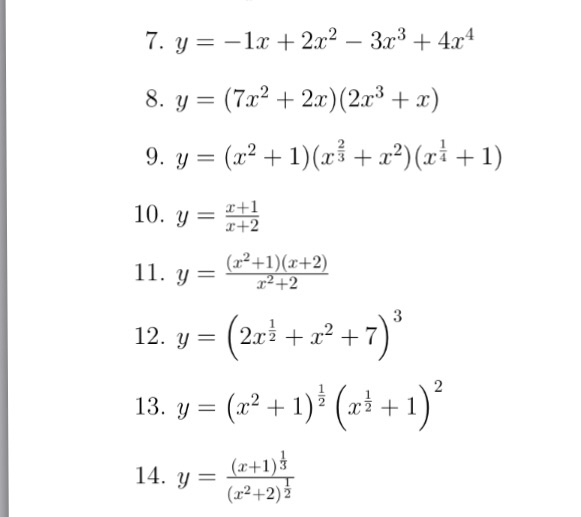



Find Dy Dx Y 1 X 2x 2 3x 3 4x 4 Y 7x 2 Chegg Com




Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com




Find Dy Dx If Y X 2 1 X 2 1 Brainly In




Ex 5 7 12 If Y Cos 1 X Find D 2y Dx 2 In Terms Of Y Alone



1
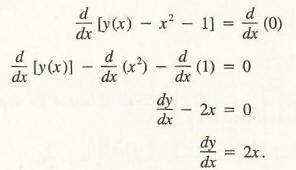



Find A Derivative With Step By Step Math Problem Solver
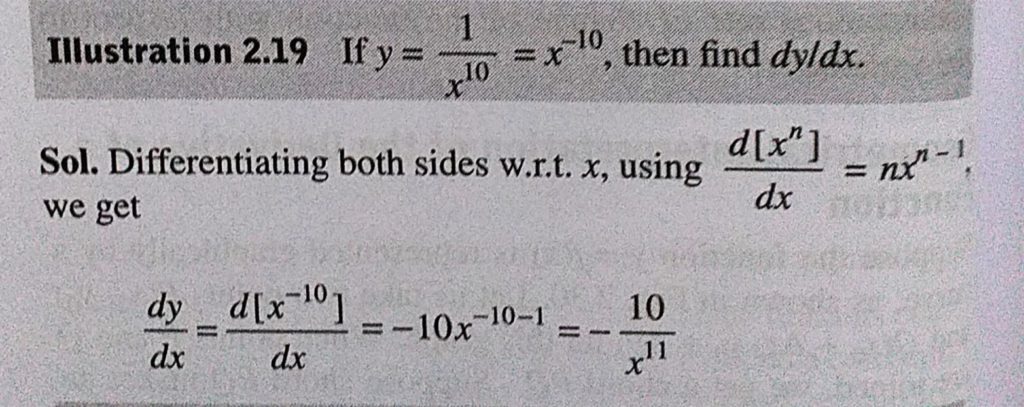



If Y 1 X 10 X 10 Then Find Dy Dx Sahay Lms



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf




If Y 1 X Then Dy Dx Is Youtube




If X Y Y X Then Find Dydx



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap16 Calculus Ab Q4 Pdf
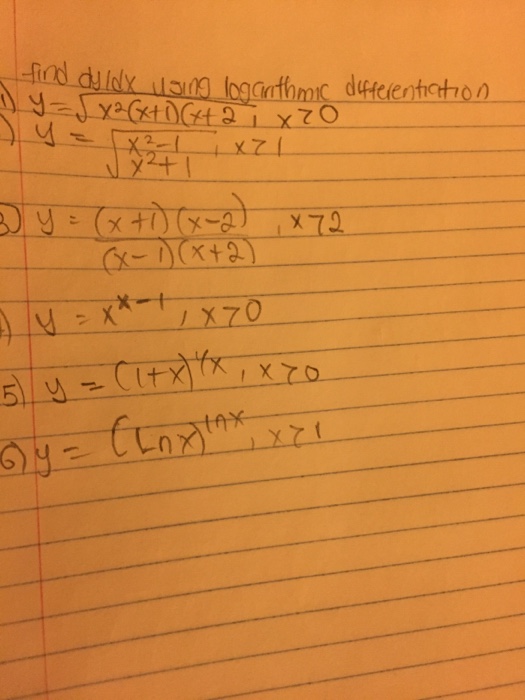



Find Dy Dx Using Loganthmic Differentiation Y Chegg Com




If Y 1 X Find Dy Dx Also Find The Value Of X




Answered Find Dy Dx For The Following 1 Y X Bartleby
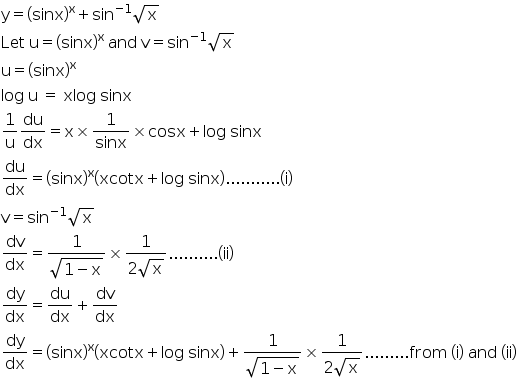



If Y Sinx X Sin 1 X 1 2 Find Dy Dx Explain In Great Detail Do Not Go Shortcut Mathematics Topperlearning Com W0t3auii




If Y Sqrt X 1 Sqrt X Then Dy Dx At X 1 Is Equal To Youtube




If Y X 1 X Show That X 2 Dy Dx Xy 2 0
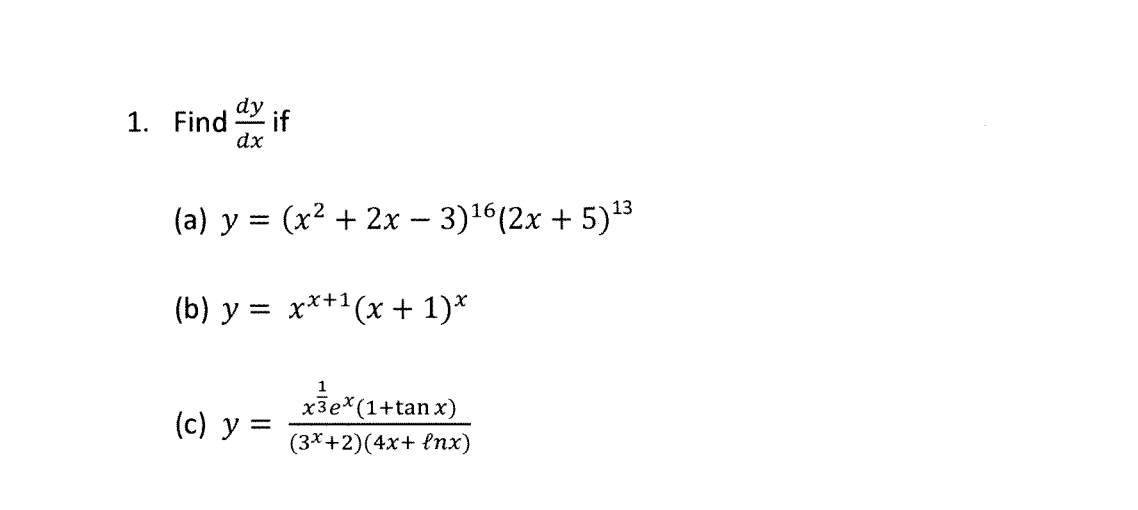



Find Dy Dx If Y X 2 2x 3 16 2x 5 13 Y Chegg Com




If Y Cos 1 1 X 1 X Then Find Dy Dx Youtube



Find Dy Dx If Y Cosx X Sinx 1 X Sarthaks Econnect Largest Online Education Community



1




Ex 5 3 9 Find Dy Dx In Y Sin 1 2x 1 2x2 Chapter 5




If Y X What Is Dy Dx Quora




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




Y X 2 Cotx 1 X 2 Find Dy Dx Youtube



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora




Iit 19 Find Dy Dx If Y F 2x 1 Square X 1 And F X Sin Square X Youtube
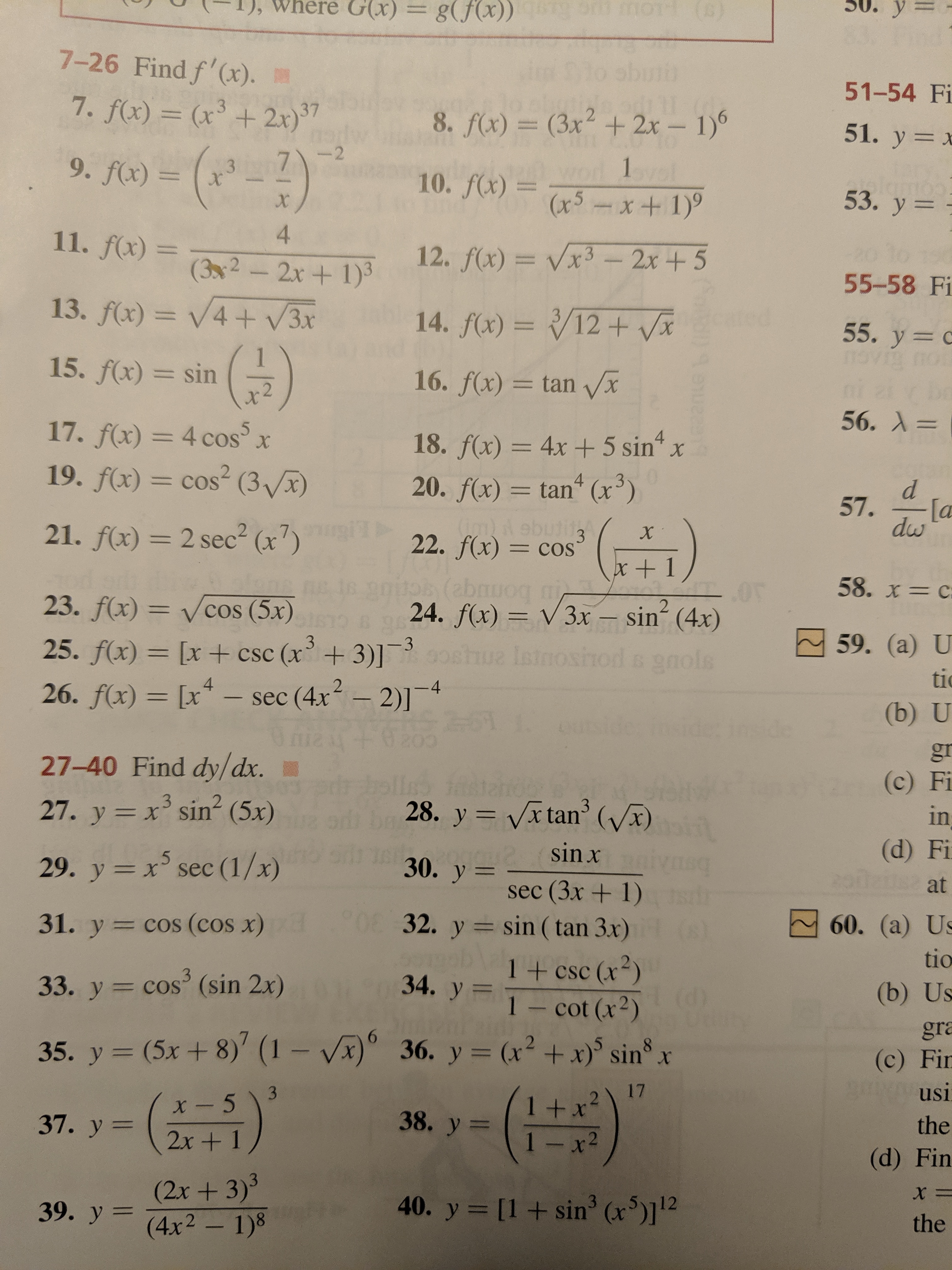



Answered G X U G Fx 00 O 7 26 Find F X Bartleby



If X Y Y X What Is Dy Dx Quora
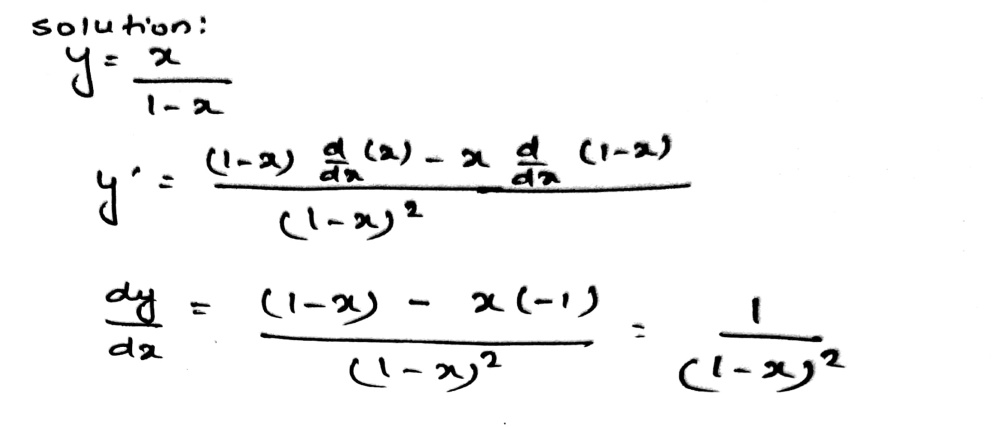



Given Y X 1 X Find Dy Dx From First Principl Gauthmath




Find Dy Dx Of Y 1 1 X X




If Y X 1 X 1 X 5 Then Dy Dx Youtube




If Y X X 1 X 2 Then Dy Dx Is Brainly In




Find Dy Dx If Y X Cot 1 X Y Brainly In




If Y X 1 X Find Dy Dx Youtube




Find Dy Dx If Y X 1 X 2


